The Ultimate Merkle Tree Guide in Solidity

Everything you need to know about Merkle trees and their future

Most of you probably have heard of Merkle trees by now. They are used everywhere in the world of blockchain.

But are you really sure exactly

How they work?
What the best ways to use them are?
What the future holds for Merkle trees?

This is not a Merkle tree.

What are Merkle Trees?

Ralph Merkle invented Merkle trees already in 1979. The most important concept to understand is a Merkle tree. This is a Merkle tree:

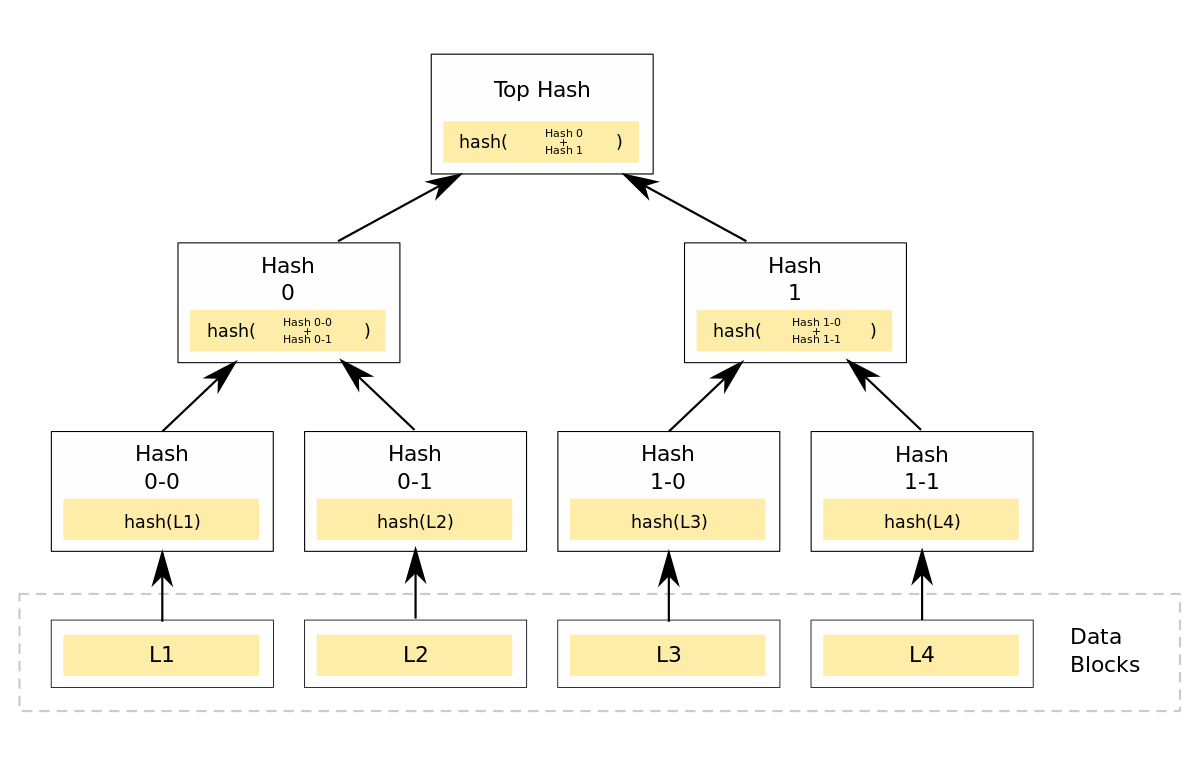
At the root of the Merkle tree is the root hash. It's created by hashing all its original values as leaf nodes. Now two leaf hashes are combined by creating a new hash just for those together. We do this all the way until we have one tree with a single root hash.

A Merkle proof now is a way for you to prove to someone who only knows the root hash that any value is in fact part of this tree as one of the leafs. For example you could prove that L3 did indeed contain a given value. All one needs to do is provide the Hash 0, Hash 1-1 and the L3 block itself. Now for the proof verification one can compute the hash of L3, then the hash 1 and finally the top hash. We can then compare the root hash against our known root hash. For a visual explanation of a Merkle proof, check out this great explanation.

As you can see for a successful Merkle proof, you need to provide all sibling nodes at every tree level. Keep that in mind as we could potentially improve upon that later in this post.

Why is this enough? Because when using a secure hash function like keccak256, it's practically impossible to create a hash collision, meaning although you reduce an infinite potential input space to just 256 bits, the likelihood that you find two different sets of inputs which result in the same hash is so low that it simply won't happen in practice. Now if you receive a matching root hash in the Merkle proof, you know this one item really must have been part of the original root hash calculation.

Merkle Proof in Solidity

The MerkleProof.sol from the Openzeppelin contracts is a great way to get started. So let's take a look how they implement it:

verifyCalldata takes in the proof itself as bytes32 array, the Merkle root hash and the leaf we want to verify for inclusion. Typically the root will be data you store in the smart contract and proof will be the data from someone created off-chain, proving to the contract that the leaf was part of the original tree.

So now processProofCalldata will iterate through each element in the proof array.

We start by taking the leaf node.
Then in each step we update our computed hash by hashing it with the next element in the proof.
1. Hashing both hashes together will always take the smaller value first.
2. Openzeppelin uses assembly with the keccak256 opcode for more efficient hashing. Alternatively one could use Solidity: keccak256(abi.encodePacked(a, b)).
We return the computed hash.

Then back in verifyCalldata we simply verify that the computed hash matches the expected root hash.

function verifyCalldata(
    bytes32[] calldata proof,
    bytes32 root,
    bytes32 leaf
) internal pure returns (bool) {
    return processProofCalldata(proof, leaf) == root;
}

function processProofCalldata(
    bytes32[] calldata proof,
    bytes32 leaf,
) internal pure returns (bytes32) {
    bytes32 computedHash = leaf;
    for (uint256 i = 0; i < proof.length; i++) {
        computedHash = _hashPair(computedHash, proof[i]);
    }
    return computedHash;
}

function _hashPair(bytes32 a, bytes32 b)
    private
    pure
    returns(bytes32)
{
    return a < b ? _efficientHash(a, b) : _efficientHash(b, a);
}

function _efficientHash(bytes32 a, bytes32 b)
    private
    pure
    returns (bytes32 value)
{
    assembly {
        mstore(0x00, a)
        mstore(0x20, b)
        value := keccak256(0x00, 0x40)
    }
}

Merkle Proofs in Bitcoin

In the blockchain world Merkle proofs date back to the very beginning, the release of the Bitcoin PDF in 2008 to prove transaction inclusions. It detailed a mechanism to verify transaction status for light clients that don’t have the full blockchain downloaded, Simplified Payment Verification (SPV).

Bitcoin light clients, in contrast to full nodes, only download the block headers of the blockchain. A block header is quite small and only contains the previous block root hash, current block root hash, timestamp, difficulty and a nonce. This allows even mobile devices to participate in the network without requiring massive amounts of data storage.

To figure out if a payment is included in the blockchain, simply ask a full node that has the blockchain downloaded for a Merkle proof. The full node can look for the block which has the transaction included and then create a Merkle proof showing that this specific transaction results in the to the light client known block root hash.

Nice, so now a light client can verify payments itself without downloading the full blockchain. But what about more complex things like state in Ethereum?

Merkle Proofs in Ethereum

Now for Ethereum we have also smart contract state. In addition to the transaction inclusion Merkle proofs, there is a second state root hash which allows proving that an account had a particular Ether balance at a given block. And alternatively also that a smart contract had a particular state in a given block. And there is a third root hash in Ethereum for logs. It allows proving that a particular event happened in that block.

We are going to take a look on how to use these special Ethereum root hashes in Merkle proofs later. But of course we can also create our own root hashes and use them in our smart contract. There are many ways to do this. Let’s explore some…

1. Efficient Airdropping

One common use case for Merkle trees are airdrops, since Merkle proofs allow us to very efficiently implement ERC20 token airdrops. The implementation is rather simple using above mentioned Openzeppelin MerkleProof library.

contract MerkleDistributor {
    address public immutable token;
    bytes32 public immutable merkleRoot;

    mapping(address => bool) public isClaimed;

    constructor(address token_, bytes32 merkleRoot_) {
        token = token_;
        merkleRoot = merkleRoot_;
    }

    function claim(
        address account,
        uint256 amount,
        bytes32[] calldata merkleProof
    ) external {
        require(!isClaimed[account], 'Already claimed.');

        bytes32 node = keccak256(
            abi.encodePacked(account, amount)
        );
        bool isValidProof = MerkleProof.verifyCalldata(
            merkleProof,
            merkleRoot,
            node
        );
        require(isValidProof, 'Invalid proof.');

        isClaimed[account] = true;
        require(
            IERC20(token).transfer(account, amount),
            'Transfer failed.'
        );
    }
}

A. Creating The Merkle Distributor Contract

Let's create the distributor contract first which will hold all the tokens are alternatively could be allowed to mint new tokens.

At the core will be the claim function that takes in the user address, the amound and the Merkle proof. The Merkle root was initially stored upon deploying the contract.

Inside claim we now how to verify

that indeed the original Merkle tree contained a leaf with the values matching the account address and amount
that the user hasn't already claimed the tokens.

The first part is exactly done with the Merkle proof verification using Openzeppelin's MerkleProof.verifyCalldata. For the second part we simply store the account in a mapping to boolean.

But now how can we create this original Merkle tree and all the proofs? This is not part of Solidity and happens off-chain. Let's explore how next.

B. Creating The Merkle Tree and Proofs

We can use merkletreejs for creating the Merkle root hashes as well as getting individual proofs.

First we have to encode the addresses and parameters. Web3.js can help use with that.
Then we can use keccak256 to compute a hash over both the address and amount for each balance.
The result will be our leaf nodes that we can enter to create a new MerkleTree using merkletreejs.
We can print the full tree using merkleTree.toString().
Or we can print individual proofs or the root hash.

---------
Merke Tree
---------
└─ 399f97e5a31d2[...]c9f3379ff72
   ├─ dd3f64a1b692[...]38dfdd8578
   └─ 15e70077678[...]e7944f27e36

---------
Merkle Root: 0x399f97e5[...]f37d0379ff72
Proof 1: 0x15e7001d277[...]79440b8f27e36
Proof 2: 0xdd3f64a1877[...]38df4b9dd8578

Now the original root will be stored in the contract. So you can see it's quite cheap to do an airdrop like this, only deploy a small contract and store the root hash.

And users can create their proofs individually off-chain and receive the tokens whenever they want to.

const keccak256 = require("keccak256");
const { MerkleTree } = require("merkletreejs");
const Web3 = require("web3");

const web3 = new Web3();

let balances = [
  {
    addr: "0xb7e390864a90b7b923c9f9310c6f98aafe43f707",
    amount: web3.eth.abi.encodeParameter(
      "uint256",
      "10000000000000000000000000"
    ),
  },
  {
    addr: "0xea674fdde714fd979de3edf0f56aa9716b898ec8",
    amount: web3.eth.abi.encodeParameter(
      "uint256",
      "20000000000000000000000000"
    ),
  },
];

const leafNodes = balances.map((balance) =>
  keccak256(
    Buffer.concat([
      Buffer.from(balance.addr.replace("0x", ""), "hex"),
      Buffer.from(balance.amount.replace("0x", ""), "hex"),
    ])
  )
);

const merkleTree = new MerkleTree(leafNodes, keccak256, { sortPairs: true });

console.log("---------");
console.log("Merke Tree");
console.log("---------");
console.log(merkleTree.toString());
console.log("---------");
console.log("Merkle Root: " + merkleTree.getHexRoot());

console.log("Proof 1: " + merkleTree.getHexProof(leafNodes[0]));
console.log("Proof 2: " + merkleTree.getHexProof(leafNodes[1]));

C. Improving Gas Costs for Merkle Airdrops

We can further improve upon this mechanism by storing the mapping for already claimed tokens as bitmap. I've explained the concept of bitmaps in Solidity previously. This optimization was taken from Uniswap.

For our airdrop we can simply add the index of the balance array to the proof itself. Then, when storing the claimed status, we simply update a single bit in the new uint256 => uint256 mapping.

mapping(uint256 => uint256) private claimedBitMap;

function isClaimed(uint256 index) public view returns (bool) {
    uint256 claimedWordIndex = index / 256;
    uint256 claimedBitIndex = index % 256;
    uint256 claimedWord = claimedBitMap[claimedWordIndex];
    uint256 mask = (1 << claimedBitIndex);
    return claimedWord & mask == mask;
}

function _setClaimed(uint256 index) private {
    uint256 claimedWordIndex = index / 256;
    uint256 claimedBitIndex = index % 256;
    claimedBitMap[claimedWordIndex] = claimedBitMap[claimedWordIndex] | (1 << claimedBitIndex);
}

function claim(uint256 index, address account, uint256 amount, bytes32[] calldata merkleProof) external {
    require(!isClaimed(index), 'MerkleDistributor: Drop already claimed.');
    [...]
    _setClaimed(index);
    [...]
}

2. Launching NFTs

In a similar way to airdropping ERC20 tokens, we can use Merkle proofs to airdrop NFTs. A simple implementation which allows for airdropping multiple NFTs to a single address is shown on the right.

We first verify the claim just like for ERC20 airdrops.
Then we mint one new NFT for each single amount that should be airdropped.

This is an incomplete example, but the idea here should be clear. You may also combine it with the bitmap trick from before to save even more gas.

function _mint(
    address to, 
    uint256 amount, 
    bytes32[] calldata merkleProof
) internal virtual {
    require(!minted[to] && _verifyClaim(to, amount, merkleProof));
    minted[to] = true;

    uint256 newId = currentId;
    balanceOf[to] += amount;

    for (uint256 i; i < amount; i++) {
        _ownerships[newId] = to;
        newId++;
    }

    currentId = newId;
}

function _verifyClaim(
    address who,
    uint256 amount,
    bytes32[] memory merkleProof
) internal view returns (bool) {
    bytes32 node = keccak256(
        abi.encodePacked(account, amount)
    );
    return MerkleProof.verify(merkleProof, MERKLE_ROOT, node);
}

4. Creating Proofs Inside The Contract

I'm not sure what a use case would be for creating proofs inside a contract directly, but it's of course possible. You can use murky for this.

Create a new Merkle contract and you can call getProof on it. That's it!

Now what would be a use case? I'm not sure, let me know in the comments please.

// Initialize
Merkle m = new Merkle();
// Toy Data
bytes32[] memory data = new bytes32[](4);
data[0] = bytes32("0x0");
data[1] = bytes32("0x1");
data[2] = bytes32("0x2");
data[3] = bytes32("0x3");
// Get Root, Proof, and Verify
bytes32 root = m.getRoot(data);
bytes32[] memory proof = m.getProof(data, 2);

5. Proving Ethereum Smart Contract State

A more advanced and very powerful use case is proving smart contract state! With that we can essentially prove to a smart contract that any smart contract had a specific state in the past. Powerful stuff.

However it only works for the past 256 blocks. The reason is that the EVM can only access the block root hash of the last 256 blocks. And this root hash will be required to verify the proof. So this allows for proving state up to roughly one hour in the past.

To verify such a proof is a little more complex and requires an understanding of

Merkle-Patricia-Tries: State trees in Ethereum are not just a plain Merkle tree, instead Merkle-Patricia-Tries are used. They allow quickly calculating the new tree root after an update without recomputing the entire tree. The main idea is that the key under which a value is stored is encoded into the “path” that you have to take down the tree.
RLP-Encoding: Recursive Length Prefix (RLP) serialization is a space-efficient format for encoding data in Ethereum. You don't have to understand all its details. Since fortunately there is a Solidity RLP library you can use.

A Merkle proof works differently in a Merkle-Patricia-Trie, but you can find a full Solidity example here.

Proving smart contract state can be broken down to proving single smart contract storage slots. Combined with the RLP encoding, this is shown on the right. You can read about the storage slot concept in the Solidity docs.

And there is an RPC method since EIP-1186 called eth_getProof that helps to create such a proof.

You can find the full Solidity example here.

function extractSlotValueFromProof(
    bytes32 _slotHash,
    bytes32 _storageRootHash,
    RLPReader.RLPItem[] memory _proof
)
    internal pure returns (SlotValue memory)
{
    bytes memory valueRlpBytes = MerklePatriciaProofVerifier.extractProofValue(
        _storageRootHash,
        abi.encodePacked(_slotHash),
        _proof
    );

    SlotValue memory value;

    if (valueRlpBytes.length != 0) {
        value.exists = true;
        value.value = valueRlpBytes.toRlpItem().toUint();
    }

    return value;
}

6. Optimistic Rollups

Optimistic rollups are building on top of the previously mentioned state proving. We've explained them in detail previously, but the main idea here is

Represent smart contract states as Merkle tree
Run all transactions only on the Optimism chain
Continuously (optimistically) update the state roots on Ethereum layer 1
Optimism chain has low security, but through the state roots on Ethereum, they enable fraud proofs
- When relayer submits malicious state root and it's contested, they loose their bond.
- Fraud proofs quite gas expensive, so they really are not meant to actually be done regularly.
- Run whole transaction which is contested with prover submit any required state as state Merkle proofs.

This is where the scaling comes from, you only run transactions on layer 1 that are contested with a fraud proof. That’s the gain. Running a transaction for a fraud proof is actually more expensive than just running it on layer 1 directly.

So the scaling advantage comes solely from the fact that you won’t run 99.9% of transactions on layer 1.

The Future = Verkle Trees?

An improvement for Merkle Trees could be Verkle Trees. They are very new and not yet used in Ethereum. The main idea behind them is to reduce the proof size dramatically. Recall that a Merkle proof consists of all sibling nodes at each level going down from root to leaf. This can be a lot of data, especially for wide trees.

Verkle Trees don't require that you provide the siblings in the proof my making use of polynomial commitments. They will allow you to prove the inclusion of some data zi in a list [z0, z1, z2...]. The list here are of course the hashes of all siblings in the same level and all we care about is that our current hash is indeed a part of it. Combine it with a technique that allows multiproofs through random evaluation, and you get even more efficient Verkle Trees.

Read Vitalik's post on Verkle Trees for more details.

Ethereum has plans to upgrade their Merkle-Patricia-Tries to them in the third upgrade stage called 'The Verge'.

The Merge is Proof of Stake.
The Surge is sharding.
The Verge is Verkle trees.
The Purge is things like state expiry and deleting old history.
The Splurge is all of the other fun stuff.

Markus Waas

Solidity Developer